The fort package is useful when you need to either
perform random orthonormal transformations (i.e., random rotation
with/without a reflection) or random projections (particularly when it
is beneficial that the projections are uncorrelated).
Due to their use of fast structured transforms, these can be much
faster than performing the equivalent operations using matrix
multiplication. More specifically, fort transforms are
generally faster when working with spaces of dimensionality 64 or
larger.
This vignette exemplifies how to use the fort package,
in practice.
Basic usage
To use fort, you just need to use the
fort() function along with the usual matrix operations
(e.g., %*%, solve()):
library(fort)
# generate some random data (100 R^64 vectors)
my_matrix <- matrix(rnorm(100 * 64), nrow = 64)
# get a random orthonormal transformation from R^64 -> R^64
my_transform <- fort(64)
print(my_transform)
#> fort linear operation: R^64 -> [fft2] -> R^64
# apply the transform to the matrix
new_matrix <- my_transform %*% my_matrix
# verify isometry
# (compare Frobenius norm of matrix before/after transform)
sqrt(sum(my_matrix^2)) - sqrt(sum(new_matrix^2))
#> [1] 0
# invert transform
my_matrix_estimate <- solve(my_transform, new_matrix)
# verify inversion
# (Frobenius norm of difference should be small)
sqrt(sum(my_matrix - my_matrix_estimate)^2)
#> [1] 3.966255e-14
# get the transform in matrix format
my_transform_matrix <- as.matrix(my_transform)
fort for dimensionality reduction
One practical case in which fort can be useful is in
data-independent dimensionality reduction methods. In particular, it can
be used to implement an (approximately) orthogonal Johnson-Lindenstrauss
transform:
library(fort)
# generate high-dimensional sparse vectors
n_samples <- 1000
dim_input <- 2048
sparse_data <- matrix(as.numeric(rnorm(n_samples * dim_input) > 0), nrow = dim_input)
# we should be able to reduce the dimensionality of the space while mostly
# preserving distances
dim_output <- 128
sketching_transform <- fort(dim_input, # input dimensionality
dim_output, # output dimensionality
type = "fft2", # type of transform to use
seed = 42
) # seed for reproducibility
# reduce dimensionality of original sparse data using our transform
reduced_data <- sketching_transform %*% sparse_data
# compare dot products in both spaces
# (the second calculation should be faster)
system.time(sparse_inner <- t(sparse_data) %*% sparse_data)
#> user system elapsed
#> 1.37 0.01 1.49
system.time(reduced_inner <- t(reduced_data) %*% reduced_data)
#> user system elapsed
#> 0.10 0.00 0.09
# vectorize dot products
sparse_inner <- as.numeric(sparse_inner)
reduced_inner <- as.numeric(reduced_inner)
plot(reduced_inner ~ sparse_inner,
xlab = "Dot products in original space",
ylab = "Dot products in reduced space"
)
abline(0, 1, lty = 2)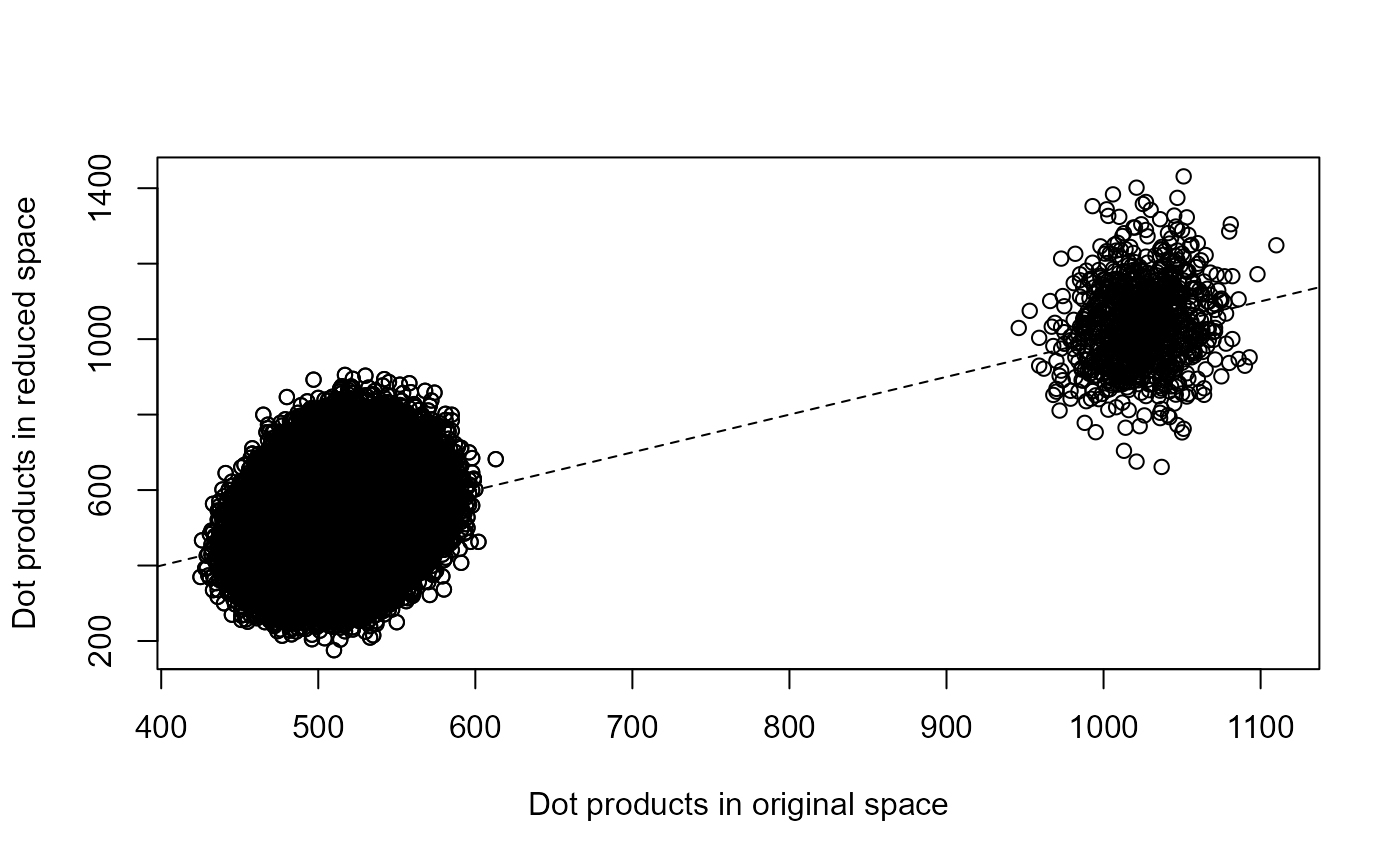
# check relative errors
summary(abs(sparse_inner - reduced_inner) / sparse_inner)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.0000001 0.0481897 0.1017553 0.1211966 0.1740701 0.7959228
# transpose matrices to comply with dist() convention
sparse_data <- t(sparse_data)
reduced_data <- t(reduced_data)
# compare distances in both spaces
# (the second calculation should be faster)
system.time(dist_original <- dist(sparse_data))
#> user system elapsed
#> 10.08 0.00 10.88
system.time(dist_reduced <- dist(reduced_data))
#> user system elapsed
#> 0.25 0.00 0.29
# vectorize distances and remove diagonal
dist_original_vec <- as.numeric(dist_original)[as.numeric(dist_original) > 0]
dist_reduced_vec <- as.numeric(dist_reduced)[as.numeric(dist_reduced) > 0]
# check relative errors
summary(abs(dist_original_vec - dist_reduced_vec) / dist_original_vec)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.300e-07 1.940e-02 4.104e-02 4.864e-02 7.014e-02 3.024e-01Thus, this example illustrates that fort can be used for
fast and (approximately) isometric data-independent dimensionality
reduction, which can be used to accelerate algorithms that rely on
calculating distances or dot products between many high-dimensional
vectors, even when typical approaches (e.g., truncated singular value
decomposition) may be too expensive.
In this particular example, we see that fort can reduce
the dimensionality of the input vectors by 16 times (which results in a
dramatic speed-up when calculating dot products or distances), while
roughly preserving the distances between vectors (typical relative
embedding errors of about 5%).
fort for kernel approximation
Another practical use case for fort is in the stochastic
approximation of kernels via the “random kitchen sinks” approach.
For example, in the case of the angular kernel, it can be
approximated (in expectation) by the dot product in a space obtained by
projecting vectors along random directions and applying a
sign() non-linearity (i.e. \(\mathbb{E}(sign(w_i^T x)sign(w_i^T y)) =
kernel_{angular}(x,y)\) if \(w_i\) are drawn from an isotropic
distribution).
While the typical approach is to use random projections here (via
matrix multiplication), it has been shown that using random orthogonal
projections (such as the ones provided by fort) can reduce
the approximation bias.
To see this in practice, let’s compare the use of fort
vs. random projections in this context:
library(fort)
set.seed(1)
n_samples <- 3000
n_groups <- 4
dim_input <- 1024
noise_level <- 0.2
# assign samples to groups and embed them in N-dimensional space
data_group <- factor(round((n_groups - 1) * runif(n_samples)))
group_effects <- matrix(rnorm(dim_input * n_groups), nrow = dim_input)
noise_matrix <- matrix(rnorm(dim_input * n_samples), nrow = dim_input)
data_raw <- group_effects %*% t(model.matrix(~data_group))
data_raw <- data_raw + noise_level * noise_matrix
# calculate angular kernel using canonical approach
# first normalize vectors, to make it easier to calculate angular kernel
data_norm <- data_raw
for (i in 1:ncol(data_norm)) {
data_norm[, i] <- data_norm[, i] / norm(data_norm[, i], "2")
}
# the cosine kernel is the same as dot product when vectors are normalized
cosine_kernel <- crossprod(data_norm)
# clamp values to the [-1, 1] range
cosine_kernel <- matrix(pmax(pmin(1, cosine_kernel), -1), nrow = nrow(cosine_kernel))
# calculate angular kernel based on cosine kernel
angular_kernel <- 1 - 2 * acos(cosine_kernel) / pi
# get approximation of angular kernel using fort (with 2x expansion)
fort1 <- fort(dim_input)
fort2 <- fort(dim_input)
angular_expansion <- rbind(fort1 %*% data_raw, fort2 %*% data_raw)
angular_expansion <- sign(angular_expansion) / sqrt(dim_input * 2)
angular_kernel_fort <- crossprod(angular_expansion)
# estimate angular kernel using random projections (with 2x expansion)
random_matrix <- matrix(rnorm(2 * dim_input^2), ncol = dim_input)
angular_expansion <- random_matrix %*% data_raw
angular_expansion <- sign(angular_expansion) / sqrt(dim_input * 2)
angular_kernel_rndproj <- crossprod(angular_expansion)
# compare both approximations with true kernel
df <- data.frame(
true_kernel = as.numeric(angular_kernel),
approximated_kernel_fort = as.numeric(angular_kernel_fort),
approximated_kernel_rndproj = as.numeric(angular_kernel_rndproj)
)
cor(df)
#> true_kernel approximated_kernel_fort
#> true_kernel 1.0000000 0.9980077
#> approximated_kernel_fort 0.9980077 1.0000000
#> approximated_kernel_rndproj 0.9960411 0.9948214
#> approximated_kernel_rndproj
#> true_kernel 0.9960411
#> approximated_kernel_fort 0.9948214
#> approximated_kernel_rndproj 1.0000000In this case, we see that using random structured orthogonal
transforms (like the ones provided by fort) provides an
approximation of the angular kernel that is faster and more accurate
than one obtained using random projections.